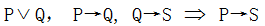c语言
hadoop
矩阵
redis
ssm
密码学
jstl
点云
题集
Tableau 技巧
xid
beautifulsoup
RHCE
C++语法,动态绑定
新媒体运营
sharding5.0.0
浮点数
mulesoft
API接口管理
飞书
离散数学
2024/4/11 19:08:22离散数学学习笔记----命题逻辑的推理理论
命题逻辑的推理理论
一些笔记:
判断推理是否正确,就是判断是否会出现1推出0的情况,如出现则推理错误,否则正确。
命题公式A1,A2,...,AkA_1,A_2,...,A_kA1,A2,...,Ak推出B的推理正确当且仅当 A1∧A2∧...,∧Ak→BA_1 \wed…
组合数学(上):数列、排列、组合
数列
取得整型数据的位数
#define LL long long
int NoD(LL x){//Number of Digitsint sum0;if(x%100) sum;while(x>0){x/10;sum;}return sum;
}整型数据各数位求和
int SoD(int x){//Sum of the Digitsint y 0;while(x > 0) { y x % 10; x / 10; }return y;
}反转数…
离散数学【详解】-自学考试湖北,争取做到识字都能看懂。
回顾8年前,我记得我大学高数没复习,考了23分。
今天公司代码写完了,明天清明节,写篇文章磨磨时间。 我的文章,没有一篇不是磨时间能好好写出来的。 ----我 先列标题,比如h1,h2,这些内容。然后往里面填字&a…
【离散数学】第一章 测试
1. A. 对 B. 错 正确答案:A 2. A. 对 B. 错 正确答案:B 3. A. 错 B. 对 正确答案:B 4.p↔q⇔p↔q A. 对 B. 错 正确答案:A 5. A. 对 B. 错 正确答案:A 6.n个命题变元组成的命题公式共有( )种不同的…
博弈论——Nim游戏
Nim游戏
通常的Nim游戏的定义是这样的:有若干堆石子,每堆石子的数量都是有限的,合法的移动是“选择一堆石子并拿走若干颗,不能不拿,如果轮到某个人时所有的石子堆都已经被拿空了,则判负(因为他…
离散数学题目收集整理练习(期末过关进度60%)
✨博主:命运之光 🦄专栏:离散数学考前复习(知识点题) 🍓专栏:概率论期末速成(一套卷) 🐳专栏:数字电路考前复习 ✨博主的其他文章:点击…
离散数学学习笔记----命题逻辑等值演算
命题逻辑等值演算
等值式
暴力方法1:判断两个公式A与B是否等职的方法,最直接就是用真值表法判断$A\leftrightarrow B $是否为重言式。
16组常用的重要等值式模式:
双重否定律 A⇔AA \Leftrightarrow \neg \neg AA⇔A幂等律 A⇔A∨AA \Lef…
离散数学学习笔记----命题逻辑的基本概念
参考书目《离散数学》屈婉玲
重要概念:
命题:非真即假的陈述句。 笔记:
悖论不是命题,如:我正在说假话。 例题1.4(2):将下列命题符号化:张晓静只能挑选202或203房间。…
SDUT-3811 离散题目17
离散题目17Time Limit: 1000MS Memory Limit: 65536KBProblem Description给出集合X和X上的关系R,求关系R在X上的对称闭包s(R)。例如:X{1,2,3,4,5} , R{<1,1>,<2,1>,<3,3>,<2,3>,<3,2>,<4,5>}s(R) {<1,1>,<…
离散数学学习笔记----集合代数
集合代数
对任何集合A,都有。 对于任何集合A,都有。 空集是一切集合的子集。 对于n元集A,子集总数为。 A的幂集表示为P(A),指A的全体子集构成的集合。 ,A与B的对称差集。其实就是。 …
高斯消元法解异或线性方程组
高斯消元法
对于一组线性方程组,枚举每一列进行如下步骤: 1、找到首元非零行 2、将这一行交换到第一行 3、将这一行的第一个数变成1,对当前这一行进行操作,不涉及矩阵的初等变换 4、将下面所有行的当前列全部消成0,利…
SDUT-2498 图结构练习——判断给定图是否存在合法拓扑序列
图结构练习——判断给定图是否存在合法拓扑序列 Time Limit: 1000MS Memory Limit: 65536KBSubmit Statistic DiscussProblem Description 给定一个有向图,判断该有向图是否存在一个合法的拓扑序列。Input 输入包含多组,每组格式如下。 第一行包含两个整…
编程的实践理论 第一章 基本理论
第一章 基本理论
我们需要的基本理论有二进制理论,数的理论和字符的理论。
1.0 二进制理论
二进制理论,也叫做布尔代数,或者是逻辑,它被设计出来用于 辅助推理因果关系,并且我们将用它来进行关于计算的因果关系 推理…
《离散数学》题库大全及答案
写在前面的一些话
这个Word是上传到CSDN的,在Office上没有乱码,WPS还没尝试过,小伙伴试过的话可以留言告诉我。我不知道为啥CSDN下载要积分,我设置的是粉丝免费下载,但是他不提醒???…
离散数学下 ---格与布尔代数
(一)目录 格的定义及性质
子格
分配格
有补格
布尔代数 (二) 内容
格的定义与性质 补充点: 格与布尔代数,它们与群的基本不同之处是:格与布尔代数的基集都是一个偏序集。 格是一个具…
离散数学——(5)间接证明法(反证法),cp规则,推理证法总结 ,谓词逻辑简介 ,谓词的概念与表示
目录 1.间接证明法(反证法) 2.cp规则
3.推理证法总结
4.谓词逻辑简介
5.谓词的概念与表示 1.间接证明法(反证法) 2.cp规则 3.推理证法总结 4.谓词逻辑简介 5.谓词的概念与表示
【离散数学必刷题】命题逻辑(第一章 左孝凌)刷完包过!
复习16题: 【1】下列哪个语句是真命题() A、今天天气真好! B、我正在说谎。 C、如果7 2 10 ,那么4 6 5。 D、如果7 2 9 , 则 4 6 5。 对于A,只有具有确定真值的陈述句才是命题…
离散数学-考纲版-02-谓词
文章目录 2. 谓词参考2.1 命题2.1 个体谓词和量词2.1.1 个体2.1.2 谓词2.1.3 量词引入个体域符号化量词真值确定谓词符号化举例示例一示例二示例三示例四 2.3谓词合式公式2.3.1 四类符号2.3.2 项2.3.3 合式公式 2.4 自由变元与约束变元2.4.1 定义2.4.2 判定2.4.3 两个规则2.4.4…
离散数学速成视频推荐(讲的不错)
【拯救者】离散数学速成(期末考研专升本) 适合人群 期末 考研 复试 转升本 月考都可以用
课程大纲 适用课本 适用于所有离散数学课本 按课本章节来, 抽取重点,翻译为人话 学习步骤: 每一章,都会【讲会考的基础💻】&a…
【离散选择题题押题】太原理工大学2021级软件工程离散结构R期末考试
1.请判断下列公式哪一个为闭式()(2分)
A.
B.
C.
D. 答案:C 要点:只要找出没有自由变元的公式即可,难度极小
以上选项是我编写出来的,大概率不会考出相同的,只是提醒…
《离散数学及其应用(原书第8版)》ISBN978-7-111-63687-8 第11章 11.1.3 树的性质 节 第664页的例9说明
《离散数学及其应用(原书第8版)》ISBN978-7-111-63687-8 第11章 11.1.3 树的性质 节 第664页的定理3的引申 定理3 带有i个内点的m叉树含有nmi1个顶点 见本人博文 内点定义不同的讨论 如果对于一个m叉正则树,即任意分支节点的儿子恰好有m个&am…
《离散数学》:代数系统和图论导论
一、代数系统
代数系统是数学中的一个重要概念,它涉及一组对象以及定义在这些对象上的运算规则。代数系统可以是抽象的,也可以是具体的。
在抽象代数中,代数系统通常由一组元素和一组操作(或称为运算)组成。这些操作…
【离散数学复习】 对于给定的集合A和B构造双射函数 f:A→B A=[PI/2, 3*PI/2],B=[-1,1]
我们可以构造以下的双射函数 f : A → B f:A\rightarrow B f:A→B: f ( x ) cos ( x − π 2 ) f(x) \cos(x-\frac{\pi}{2}) f(x)cos(x−2π)
其中 c o s cos cos 表示余弦函数。这个函数的作用是将集合 A A A 中的每个元素映射到集合 B B B 中的一个唯…
离散数学---期末复习知识点
一、 数理逻辑
[复习知识点]
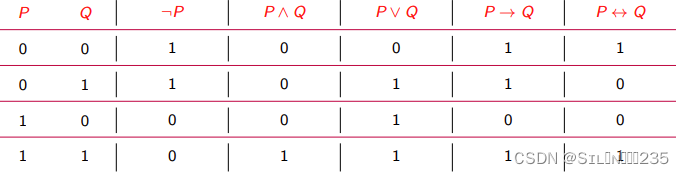
1、命题与联结词(否定¬、析取∨、合取∧、蕴涵→、等价↔),命题(非真既假的陈述句),复合命题(由简单命题通过联结词联结而成的命题)
2、命题公式与赋值(成真、成假)&#x…
【离散数学】循环群练习题
1:模n加法循环群的生成元输入循环群的阶数n,输出该群的生成元。例如:输入:24输出:1 5 7 11 13 17 19 23注:生成元用空格分隔,(23后面也有一个空格)#include <iostream…
DM@数理逻辑@命题公式及其赋值@真值表@公式分类
文章目录 abstract命题公式及其赋值命题常项命题变项 命题公式合式公式(命题公式)限定基本联结词的合适公式的定义合式公式中的0和1子公式 **公式的层次定义**分层加括号 命题公式的赋值和解释成真赋值成假赋值公式的书写规范括号的省略 真值表赋值方法数量构造真值表 公式分类…
离散数学笔记 第一章 逻辑和证明1.1
看完了北大的离散数学,现在把手中的黑书——《离散数学及其应用》——看一下。
基本内容:
1.基本符号:∧∨⊕┐↔→↑↓∧∨⊕⌝↔→↑↓优先级:┐>∧>∨>→>↔⌝>∧>∨>→>↔练习1.1:
22.…
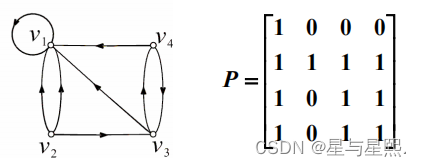
矩阵的对称性,自反性和反对称性的判断
用C语言实现离散数学中对矩阵的简单操作及对矩阵的判断
判断是否输入的矩阵是否为方阵,在是方阵的基础上判断是否具有对称性,反对称性和自反性。
对称矩阵:一个方形矩阵,其转置矩阵和自身相等。 对称矩阵是指以主对角线为对称轴…
SDUT-3364 数据结构实验之图论八:欧拉回路
数据结构实验之图论八:欧拉回路Time Limit: 1000MS Memory Limit: 65536KBSubmit Statistic DiscussProblem Description在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。能否走过这样的七座桥,并且每桥只走一次&am…
SDUT-1488 数据结构实验:连通分量个数
数据结构实验:连通分量个数Time Limit: 1000MS Memory Limit: 65536KBSubmit Statistic DiscussProblem Description在无向图中,如果从顶点vi到顶点vj有路径,则称vi和vj连通。如果图中任意两个顶点之间都连通,则称该图为连通图&am…
图灵停机问题(halting problem)
问题描述 是否存在一个过程能做这件事:该过程以一个计算机程序以及该程序的一个输入作为输入,并判断该过程在给定输入运行时是否最终能停止。问题解答 1936年图灵证明这样的过程是不存在的。证明 (反证法) 假设:存…
Python解离散数学
离散数学
离散数学是对可数的、不同的或独立的数学结构的研究。 一个很好的例子是像素。 从手机到电脑显示器再到电视机,现代屏幕由数百万个称为像素的小点组成,这些点排列成网格。 每个像素根据设备的命令以指定的颜色亮起,但每个像素只能显…
2022离散数学图论笔记03
2022离散数学图论笔记03内容预览笔记笔记内容为日常上课记录与整理,为图片格式,仅供学习。内容预览
1.无向树的定义和性质 2.欧拉图定理8.1证明 3.欧拉图定理8.3证明 4.计算生成树的个数 5.习题 6.段集空间 7.根树 8.图的矩阵表示 7.相邻矩阵和邻接矩阵…
2022离散数学图论笔记02
2022离散数学图论笔记02内容预览笔记笔记内容为日常上课记录与整理,为图片格式,仅供学习。内容预览
1.图的基本概念 2.通路与回路 3.无向图的连通性 4.无向图的连通度 5.图论重点整理 6.可图化 可简单图化 7.欧拉图 8.哈密顿图 9.习题 笔记 ——————…
离散数学学习笔记----一阶逻辑等值演算与推理
一阶逻辑等值演算与推理
一阶逻辑中的基本等值式:
第一组:16组等值式给出的代换实例都是一阶逻辑的等值式。
第二组:
量词否等等值式 ∀xA(x)⇔∃xA(x)\neg \forall xA(x) \Leftrightarrow \exists x \neg A(x)∀xA(x)⇔∃xA(x) ∃xA(x)⇔…
SDUT-2506 完美网络
完美网络Time Limit: 1000MS Memory Limit: 65536KBSubmit Statistic DiscussProblem Description完美网络是连通网络的基础上要求去掉网络上任意一条线路,网络仍然是连通网络。求一个连通网络要至少增加多少条边可以成为完美网络。Input第一行输入一个数T代表测试数…
离散数学学习笔记----一阶逻辑基本概念
一阶逻辑基本概念
一些笔记:
重言式的代换实例都是永真式,矛盾式的代换都是矛盾式。
对公式中的个体域及个体常项、函数符号、谓词符号的指定称作解释,指定自由出现的个体变项的值称为赋值。
注意解题格式。以下给出书上几道例题。
用0元…
《离散数学》:集合、关系和函数
〇、前言
这章将会对集合、以及集合之上的关系、以及两个集合之间的映射情况做一个细致的讨论。集合作为数学和其他领域中的基础概念,具有广泛的应用和重要的地位。它为数学建立了基本的体系和推理方法,为各个领域的研究和应用提供了一种统一的描述和分…
命题逻辑推理规则二十一条
如是我闻: 命题逻辑是一种形式逻辑,它用于表示逻辑表达式中事物的真假状态,并利用一系列推理规则来推导结论。以下是按照从简单到复杂的顺序整理的命题逻辑推理规则:
简单规则 蕴含消除 (Modus Ponens) 如果 p → q p \rightarr…
【GDOI2017模拟12.3】告别
Description
给出两个1~n的排列A和B,可以进行m次操作,每次操作随机选择一个三元组(i,j,k),将这个三元组所对应的数在A中进行轮换(即i->j,j->k,k->i) 求在m次操作之内将A变成B的概率,答案对99824…
《离散数学》第三章:命题逻辑(第一部分)
3.1什么是命题
3.1.1命题和非命题 注意:数理逻辑研究的中心问题是推理,而推理的前提和结论都是命题。因而命题是推理的基本 单位。 定义:具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”,称为真值。真值只有…
基于sympy实现离散数学中命题逻辑推论公式的自动证明
from sympy import symbols, satisfiable# sympy中的逻辑运算符:~否定,&合取,|析取,!异或,>>蕴含,等价# 证明题 A->B, B->C | A->C# 定义符号变量
p, q, r symbols(p q r)
# 定义命题逻…
离散数学——(1)数理逻辑,命题的概念,命题联结词,条件联结词,命题公式,命题的翻译
目录
1.数理逻辑
2.命题的概念
1.命题的判断
2.命题的真值
3.原子命题和复合命题 3.命题联结词
1.否定联结词
2.合取联结词
3.析取联结词
4.条件联结词
1.双条件联结词
5.命题公式
1.合式公式
6.命题的翻译 1.数理逻辑 2.命题的概念 1.命题的判断 2.命…
离散数学例题——4.计数和集合论(特殊关系、计数基础和函数)
等价关系 等价关系的证明 等价类和商集 等价关系与划分一一对应 偏序关系 证明偏序关系 哈斯图 整除关系画哈斯图 特殊元素
最大最小元,极大极小元 上界上确界,下界下确界 其他关系
全序关系、良序关系 拟序关系、相容关系 计数基础 排列组合 函数定义…
离散数学 学习 之 一阶逻辑基本概念 (一 )
个体词可以 理解为主语 , 3 不是偶数 ,3 就是 个体常项 凡整数都能被 2 整除 , 整数就是 个体变项 上面的谓词是 ( 1 ) 是无理数 ( 2 ) 是有理数 ( 3 ) 与 同岁 …
Prolog 中的逻辑探险:学习9组逻辑蕴涵公式
引言
上次写了16组等价公式定律,今天继续用Prolog写9组逻辑蕴涵公式。 感觉这些公式的名称与公式挺难一一对应来记忆的,只能多练习了.
1. 附加律 (Addition)
A ⇒ A∨B 当你拿到一个苹果(A),突然你知道,即使有了梨(…
【笔记】【电子科大 离散数学】 2.命题
文章目录 数理逻辑定义 命题定义不是命题的例子 原子命题和复合命题定义约定 命题联结词否定联结词定义例子真值表 合取联结词定义例子真值表 析取联结词定义例子 蕴含联结词定义例子真值表 等价联结词定义例子真值表 命题符号化及其应用速查表格优先级复合命题符号化布尔检索演…
组合数学(下):概率、博弈
概率
有限概率
👉饱和式救援
【题目】 空间限制: 65536K ● 题目描述 在《流浪地球》电影中,地球上大部分的行星发动机被摧毁。 人类再一次展开全球性救援,现在告诉你每只救援队的目标发动机的编号以及这只救援队在成功救援的概…
离散数学 学习 之 一阶逻辑基本概念 ( 四 )
好好理解这个 代换实例,每个 谓词公式 都替换一个 命题公式 在蕴含式 中 ,只有前式 为 假 ,后式 为 真,这个式才是假的 ,可以利用 这个进行判断 找个 成真解释 ,找个 成假 解释 不能 替换 才去 找 解释 &…
【离散数学必刷题】谓词逻辑(第二章 左孝凌版)刷完包过!
专栏:离散数学必刷题 本章需要掌握的重要知识: 1.利用谓词表达式表示命题 2.变元的约束 3.谓词公式的定义、谓词公式的赋值 4.谓词公式的翻译(注意在全总个体域时使用特性谓词) 5.有限论域上量词的消去 6.谓词公式中关于量词的等价…
DS@命题公式等值演算@常用等值式模式
文章目录 abstract等值式等值的判断真值表法等值演算法 任意置换命题重言式和矛盾式的置换性质性质 等值模式常用等值式模式 等值演算等值演算置换规则等值式模式的代入实例等值演算示例 小结 abstract
命题公式等值演算常用等值式模式
等值式 A ⇔ B A\Leftrightarrow{B} A⇔…
# 学习 Prolog 和 离散逻辑的16个等价公式:一趟有趣的逻辑之旅
Prolog 的语法很奇怪,需要一些时间来适应,所以我花了点时间,想用Prolot来学习和验证离散逻辑的16组等价公式。
1. 双重否定律 (Double Negation Law)
A ⇔A 首先,我们来看看双重否定律。在 Prolog 中,我们可以这样验证它:
fun1(A,Z):-memb…
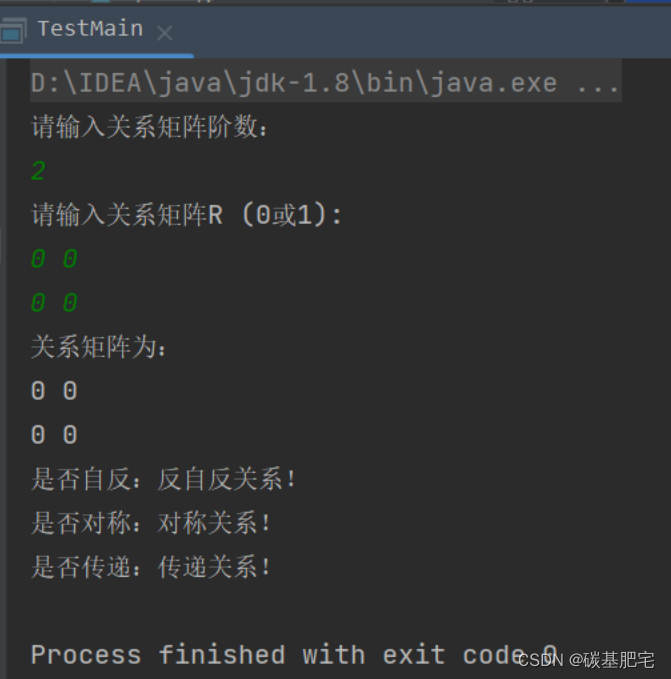
离散数学实践(2)-编程实现关系性质的判断
*本文为博主本人校内的离散数学专业课的实践作业。由于实验步骤已经比较详细,故不再对该实验额外提供详解,本文仅提供填写的实验报告内容与代码部分,以供有需要的同学学习、参考。 -------------------------------------- 编程语言ÿ…